Recent interest in human brain connectivity has led to the application of graph theoretical analysis to human brain structural networks, in particular white matter connectivity inferred from diffusion imaging and fiber tractography. While these methods have been used to study a variety of patient populations, there has been less examination of the reproducibility of these methods. A number of tractography algorithms exist and many of these are known to be sensitive to user-selected parameters. The methods used to derive a connectivity matrix from fiber tractography output may also influence the resulting graph metrics. Here we examine how these algorithm and parameter choices influence the reproducibility of proposed graph metrics on a publicly available test-retest dataset consisting of 21 healthy adults. The dice coefficient is used to examine topological similarity of constant density subgraphs both within and between subjects. Seven graph metrics are examined here: mean clustering coefficient, characteristic path length, largest connected component size, assortativity, global efficiency, local efficiency, and rich club coefficient. The reproducibility of these network summary measures is examined using the intraclass correlation coefficient (ICC). Graph curves are created by treating the graph metrics as functions of a parameter such as graph density. Functional data analysis techniques are used to examine differences in graph measures that result from the choice of fiber tracking algorithm. The graph metrics consistently showed good levels of reproducibility as measured with ICC, with the exception of some instability at low graph density levels. The global and local efficiency measures were the most robust to the choice of fiber tracking algorithm.
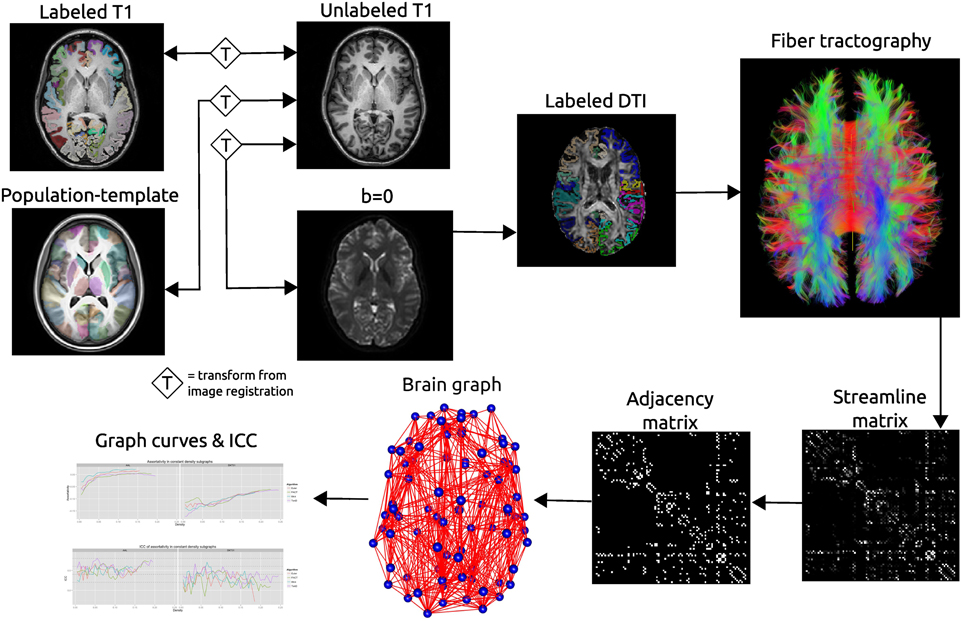
Schematic of the network processing scheme. Image registration is used to find transformations between the T1 image and: the T1 image for that subject’s other time point; the population template; the b = 0 image acquired as part of the DTI acquisition. Labels are transformed into the DTI space where fiber tractography is performed. A matrix is created that records the number of streamline connecting each pair of labeled regions. This matrix is thresholded as constant density to create an adjacency matrix which defines connections in a brain graph. Graph curves are generate by calculating network summary measures over a range of density values and ICC plots are used to examine the reproducibility of the metrics.